Measuring and Improving BERT's Mathematical Abilities by Predicting the Order of Reasoning
Piotr Piękos1, Henryk Michalewski1,2, Mateusz Malinowski3
1University of Warsaw, 2Google, 3DeepMind
Have you ever tried to do mathematics with pre-trained language models? It turns out that even the most basic questions can be very challenging for them. A simple question requiring basic addition or other elementary operation can bamboozle an otherwise very well prepared model but don't trust us, try it yourself.
We would, however, expect such models to possess some mathematical abilities. As an example language model to investigate, we choose BERT. We scrutinize its mathematical abilities and suggest that self-supervised training on explanations of how the answer to a given mathematical question was derived can improve mathematics in language models. We also suggest a new loss for utilization of the explanations. As a benchmark for measuring mathematical skills, we use AQuA-RAT. AQuA-RAT is a data set with math word problems in the form of a closed test. Each data point consists of a question, possible answers, and the information which answer is correct. What's specific to AQuA-RAT is that it is augmented by a rationale - an explanation of how the solution was derived. We use that for self-supervised training, and
we don't use rationales for fine-tuning.

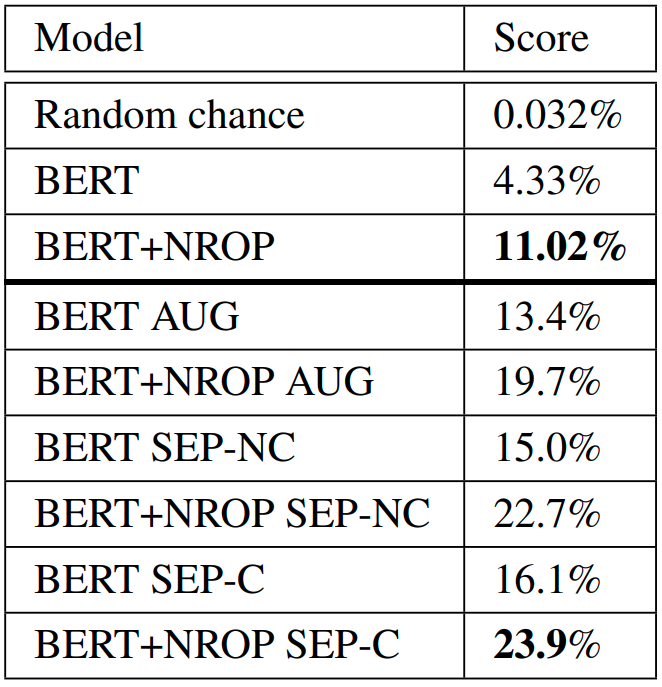
We Hypothesize that we can improve mathematics in language models by additional training on rationales. They are a step-by-step derivation of the solution. Therefore, they might contain natural language, a mix of natural language with formal mathematics, and purely formal expressions. Because of that model can learn to deal with mathematics in natural language environments. We also suggest a novel loss that works on rationales - Neighbor Reasoning Order Prediction (NROP). It is a coherence loss that forces the model to focus more on the rationale. In the NROP task, the model has to predict whether two randomly chosen neighboring rows have been swapped. For 50% of rows, two neighbor rows are swapped and for 50%, rationale stays original. The model has to predict whether the swap occurred or not. NROP loss is combined with standard MLM loss for self-supervised training.
Interestingly, for MLM loss, there are parallels between masking numbers and solving mathematical equations, where it can be seen as solving the equation with unknown.
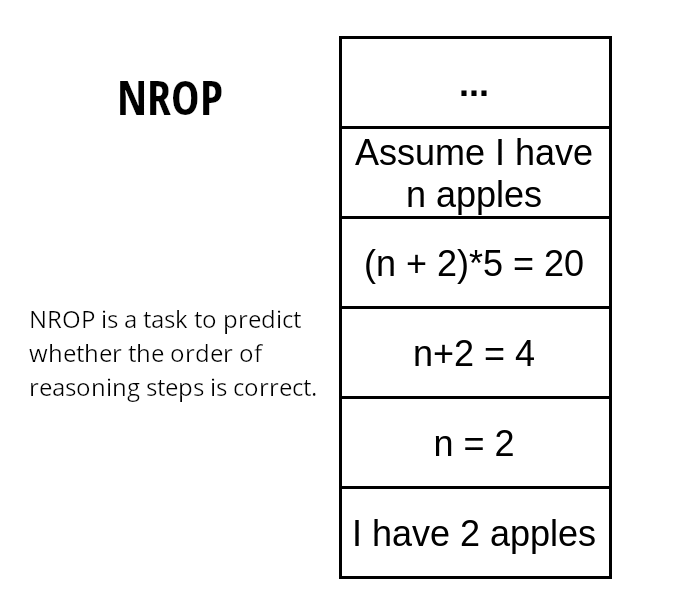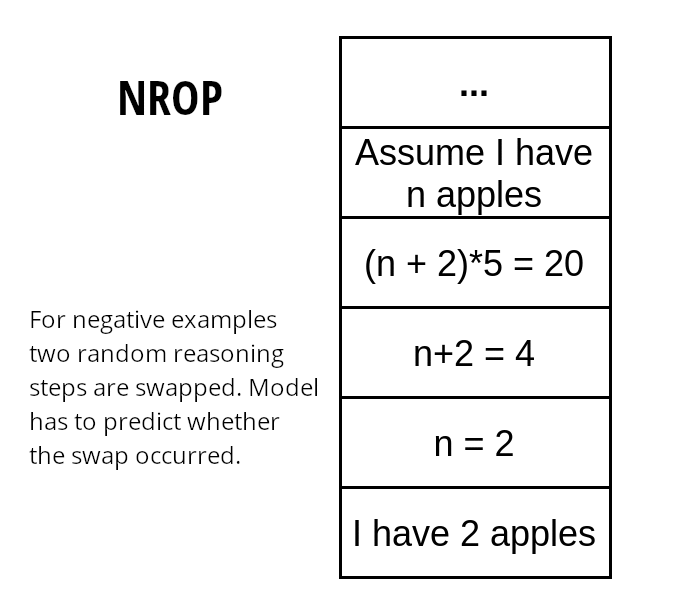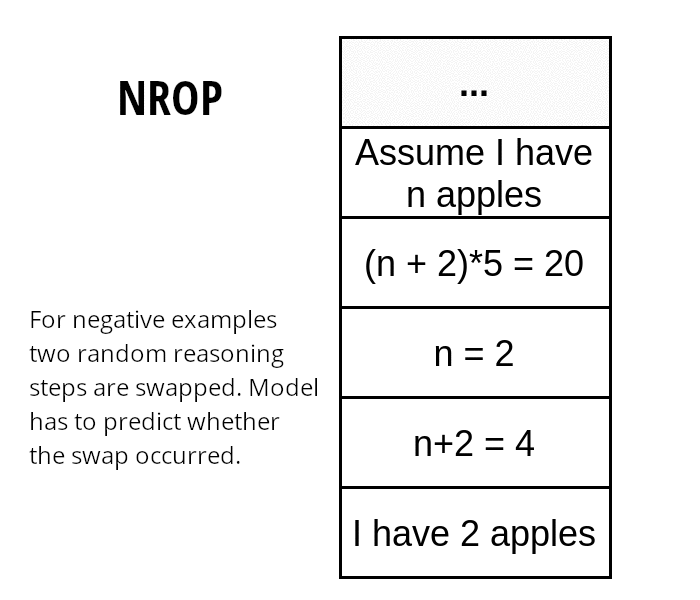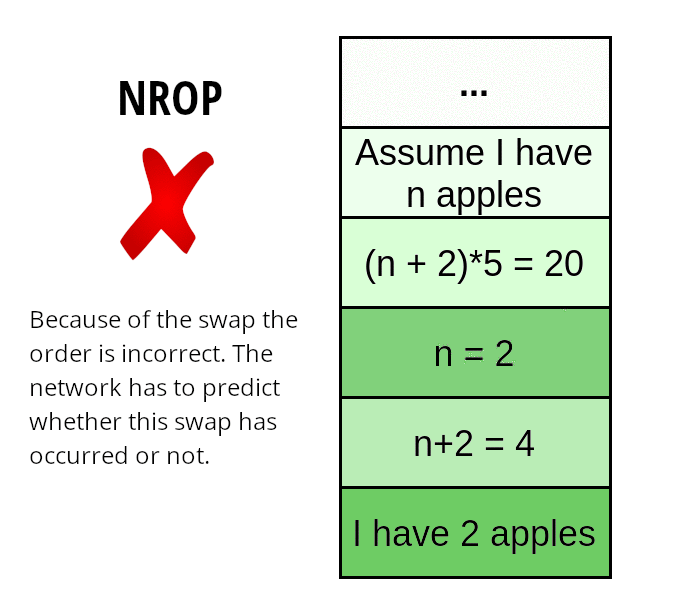
We wanted to measure the impact of using rationales and how much our loss helps with the utilization. To measure that, we conducted four experiments:
- BERT-base: Directly fine-tuned BERT to predict the correct answer.
- BERT-AQuA: BERT with additional MLM training only on questions.
- BERT-AQuA-RAT: BERT with additional MLM training on questions combined with rationales.
- BERT-NROP: BERT with both MLM and NROP with training on questions combined with rationales.
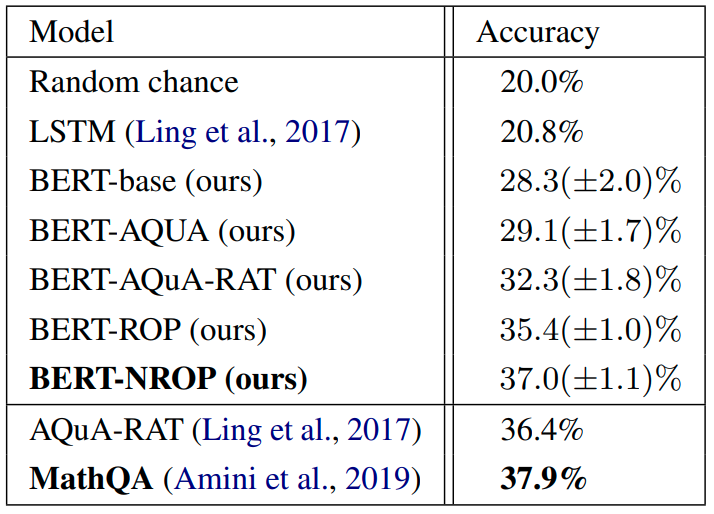
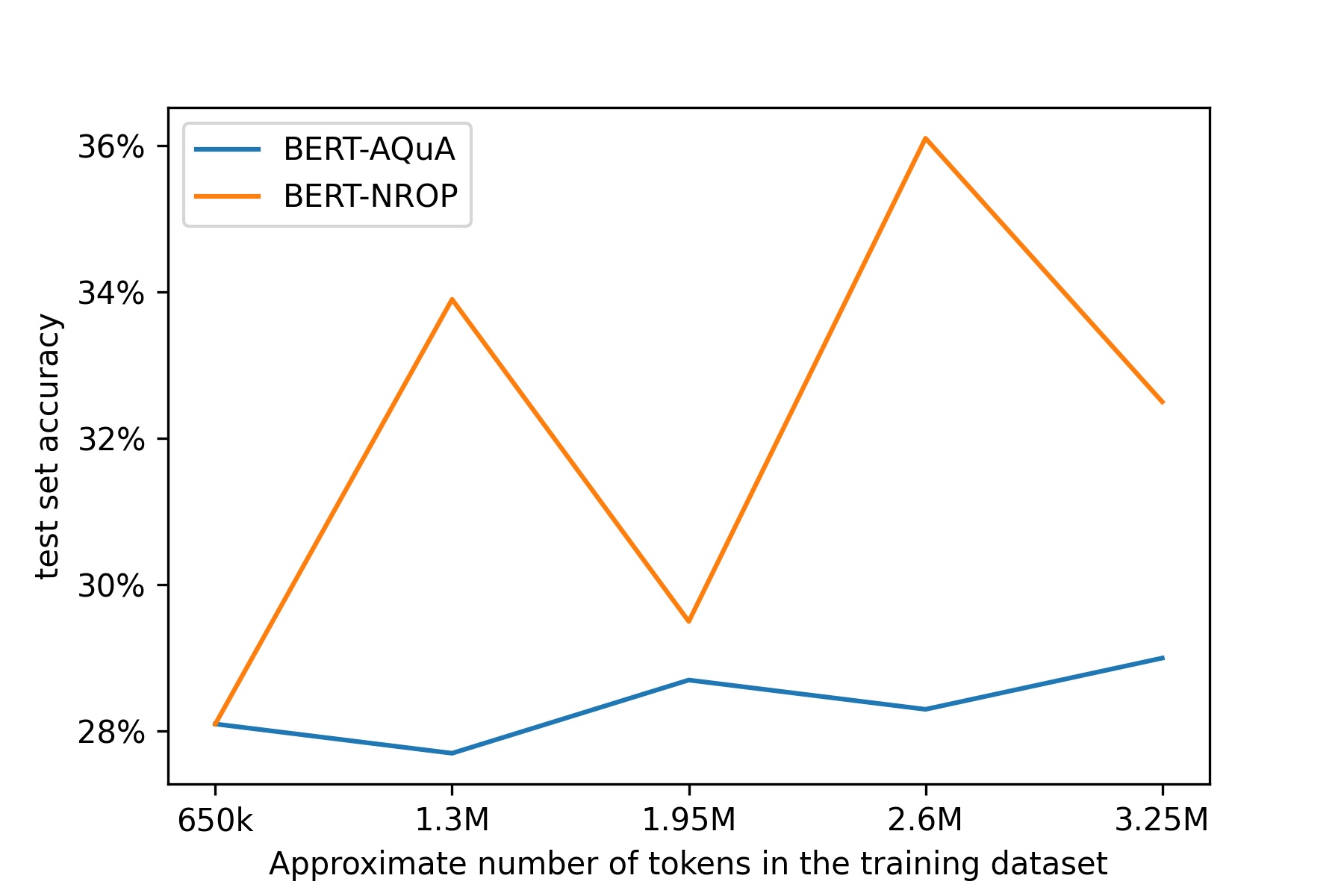
You could, however, argue (and rightfully so) that the improvement in BERT-AQuA-RAT in comparison to BERT-AQuA doesn't necessarily have to be caused by some intrinsic quality of rationales for training. BERT-AQuA-RAT simply has access to more data than BERT-AQUA because it has access to the same questions with the addition of the rationale.
We measured that question with rationale has around 3 times more tokens than just question alone. Therefore, to make a fair comparison between the two models, we have to make samples with 3 times more rows for training without rationale than for training with rationale - that will create a similar number of tokens for self-supervised training in both scenarios. We compared them in setups with increasing numbers of tokens available for pretraining. We found that in this setup too, rationales improve the results outperform BERT-AQuA showing that rationale tokens were utilized much better than question tokens and that they indeed are qualitatively better for learning mathematical skills.
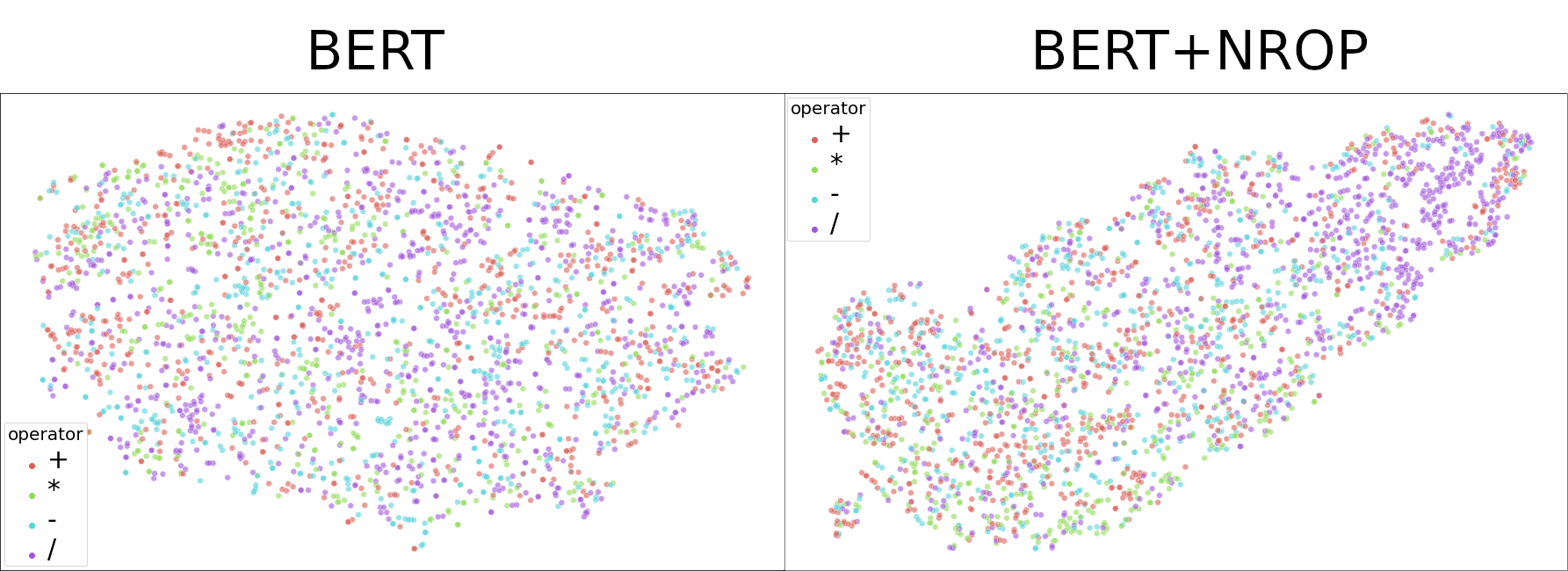
Embeddings
After investigating the models further, we found other observations. First of all, BERTs embeddings, even after fine-tuning to predict the correct answer, had no information about basic operators. Interestingly, BERT-NROP seems to retrieve some information about them.
We wanted to look at specific examples of what questions does BERT solve and what he does not. However, random guessing on AQuA-RAT yields 20% accuracy, which would make it hard to distinguish solved questions from pure luck. With that in mind, we have constructed a new evaluation task - the permutation consistency test. Each question is copied five times with the correct answer at a different position. Model scores one point only if it solves all five questions. Therefore the random chance in this experiment is lower than one-tenth of a percentile. In this test, our model solved three times as many questions as BERT.
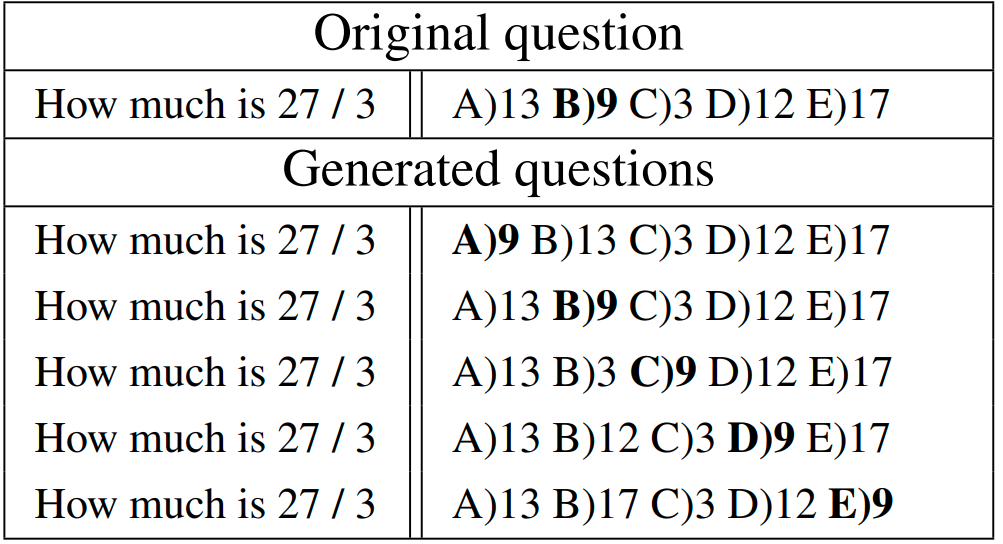
We found that in most of the questions solved by BERT answer was either round or in another way different than the other candidates. We did not find a similar pattern in questions solved by BERT-NROP.
Results of the permutation consistency test suggest that models also rely strongly on the order of the answers. Names presented here are our models that rely on permutation invariant losses. Their goal is to increase the score on the permutation invariant test while keeping the original test score at a good level. You can find more details about them in the paper.
To better understand the models' performance, we check which questions are difficult for the model. We categorize questions by their difficulty for BERT-NROP and BERT. To estimate a question's difficulty, we have ranked the candidate answers according to the model's uncertainties. For instance, if the correct answer has the second-largest probability, we assign to that question difficulty two. With that method, we group questions into five difficulty categories. Manual inspection shows that for BERT+NROP, these groups show somewhat expected patterns ranging from single operations to number theory problems or those that require additional knowledge. We did not observe a similar pattern for BERT, except the easiest group, where the model chooses the answer that is somewhat different from the other candidates.
We confirmed this observation by conducting a human study. It is described in detail in the paper.
Publications
This research was presented at the following conferences and workshops:- ACL-IJCNLP 2021, Oral Presentation
- MathAI 2021 (ICLR Workshop)
- EEML 2021, Best Poster Award
- BayLearn 2020, Title: Learning to reason by learning on rationales